■ 4장 : 다양한 분류 알고리즘 (럭키백 확률 계산)
☞ 로지스틱 회귀, 확률적 경사 하강법과 같은 분류 알고리즘 배우기
☞ 이진분류와 다중 분류의 차이를 이해하고, 클래스별 확률 예측하기 학습하기
이전장 까지 지도학습의 (분류:Classcification / 회귀 : Regression)을 학습하였다.
여기에서 좀더 다른 알고리즘을 배우는것 같다.분류에서는 이진분류 / 다중분류를 배우고→ (분류를 하는 기준이 좀더 다른 방법을 배울것 같고)회귀에서는 로지스틱 회귀, 경사 하강법을 배울것 같다.
→ (정확한 값을 알수 없기에 데이터에 특성에 따라서 로지스틱, 경사 하강 같은 기법을 배울것 같다)
목차만 보고 예상을 한 것이니, 세부 사항은 실제 학습 내용과 다를수 있다.
→ 로지스틱 회귀는 분류 모델 기법이였다.!! (여기서 이중/다중분류를 배우고 적용한다)
■ 로지스틱 회귀 : 키워드로 둘러보기
☞ 키워드 : 다중분류, 시그모이드 함수, 소프트맥스 함수
책에 나와있는 키워드 중에 어디서 들어본 단어 -> 시그모이드 함수, 소프트맥스 함수
딥러닝구조
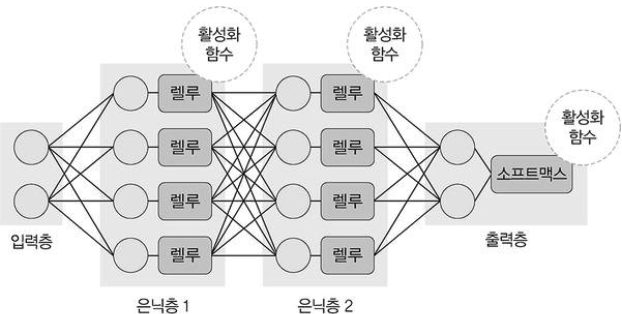
· 딥러닝에 활성화 함수가 여러가지 있는데, 그중에 포함되는 함수!!
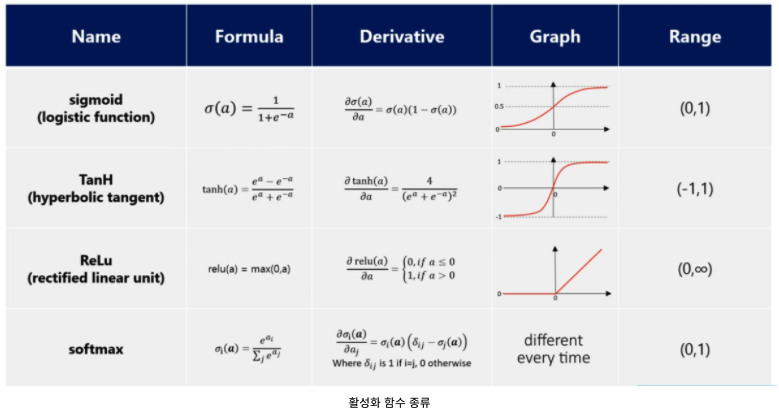
· 활성화 함수에는 아래와 같은 종류가 있다.

■ 로지스틱 회귀
정의 : 이름은 회귀지만, 분류 모델입니다.
선형 방정식을 사용한 분류 알고리즘입니다.
선형 회귀와 달리 시그모이드 함수, 소프트맥스 함수를 사용하여 클래스 확률을 출력 할수 있다.
이진 분류 : 하나의 선형 방정식을 훈련 → 시그모이드 함수 (0~1사이값 생성) → 양성/음성 클래스 확률
다중 분류 : 여러개의 클래스 개수만큼 방정식을 훈련 → 소프트맥스 함수 (전체 클래스의 합이 항상 1) → 각 클래스에 대한 확률
- 다중분류 : target데이터 (train_target)에 2개 이상의 클래스가 있는 경우
- sklearn에서는 문자열을 그대로 사용가능 (defautl : 알파벳순으로 정렬)
- 확률을 구할때 0~1사이의 값으로 구성되어야 한다.
- 아주 큰 음수가 0이 되고 && 아주 큰 양수가 1이 되어야 한다.
- 시그모이드 함수(sigmoid fuction) 또는 로지스틱 함수 (logistic function)을 사용하면 가능
- 시그모이드 함수는 하나의 선형 방정식의 출력값을 0~1사이로 압축합니다.


- 소프트맥스 함수 (p.190)
- 여러개의 선형 방정식의 출력값을 0~1사이로 압축하고, 전체 합이 1이 되도록 만듭니다.
- 이를 위해서 지수 함수를 사용하기 때문에, 정규화된 지수 함수라고 부릅니다.
- 시그모이드 함수(1개의 선형방정식) vs 소프트맥스 함수(여러개의 선형방정식)
■ 확률적 경사 하강법
☞ 키워드 : 손실 함수, 에포크 (딥러닝쪽에서 응용계층에서 들어본것 같다)
☞ 신경망 알고리즘을 바로 사용합니다. ( ≫ 확률적 경사 하강법이나 미니배치 경사 하강법을 사용 )
☞ "데이터를 한번에 모두 읽어 올 수 없기 때문에, 데이터를 조금씩 점진적으로 학습하는 방법"
- 확률적 경사____ 하강법_________
"무작위", "랜덤" "기울기" "내려가는 방법" - 에포크
- 훈련세트를 한번 모두 사용하는 과정
- 미니배치 경사 하강법
- 여러개의 샘플을 사용해 경사하강법을 수행하는 방식
- 배치 경사 하강법
- 한번에 경사로를 이동하기 위해서 전체 샘플을 사용
- 손실함수
- 샘플 하나에 대한 손실을 정의
- 비용 함수 : 훈련 세트에 있는 모든 샘플에 대한 손실함수의 함
- 손실함수 ⊆ 비용함수
■ 기본 미션
문제) 로지스틱 회귀가 이진 분류에서 확률을 출력하기 위해 사용하는 함수는 무엇인가요?
① 시그모이드 함수
② 소프트맥스 함수
③ 로그 함수
④ 지수 함수
답) 1번, 이진분류의 경우 1개의 선형방정식을 0~1사이값 생성합니다.
■ 선택 미션

'study' 카테고리의 다른 글
| 혼공 머신러닝/딥러닝 6주차 (0) | 2022.02.26 |
|---|---|
| 혼공 머신러닝/딥러닝 5주차 (0) | 2022.02.18 |
| 혼공 머신러닝/딥러닝 4주차 (0) | 2022.02.10 |
| 혼공 머신러닝/딥러닝 2주차 (0) | 2022.01.17 |
| 혼공 머신러닝/딥러닝 1주차 (0) | 2022.01.15 |



