■ 기본미션
☞ p. 279의 확인 문제 5번 풀고 인증하기

■ 선택미션
☞ Ch.04(04-1)에서 배운 8가지 기술통계량(평균, 중앙값, 최솟값, 최댓값, 분위수, 분산, 표준편차, 최빈값)의 개념을 정리하기
다양한 기술적인 통계량을 한번에 조회할수도 있습니다.
describe()를 통해서 한번에 조회가 가능하며, 25%, 70%의 사항은 default값으로 사용자가 범위를 조절하고, 갯수도 늘릴수 있습니다.
# 아래와 같은 코드로 수행하면 30%, 60%, 90% 지점의 놓인 값을 표시합니다.
ns_book6.describe(percentiles=[0.3, 0.6, 0.9])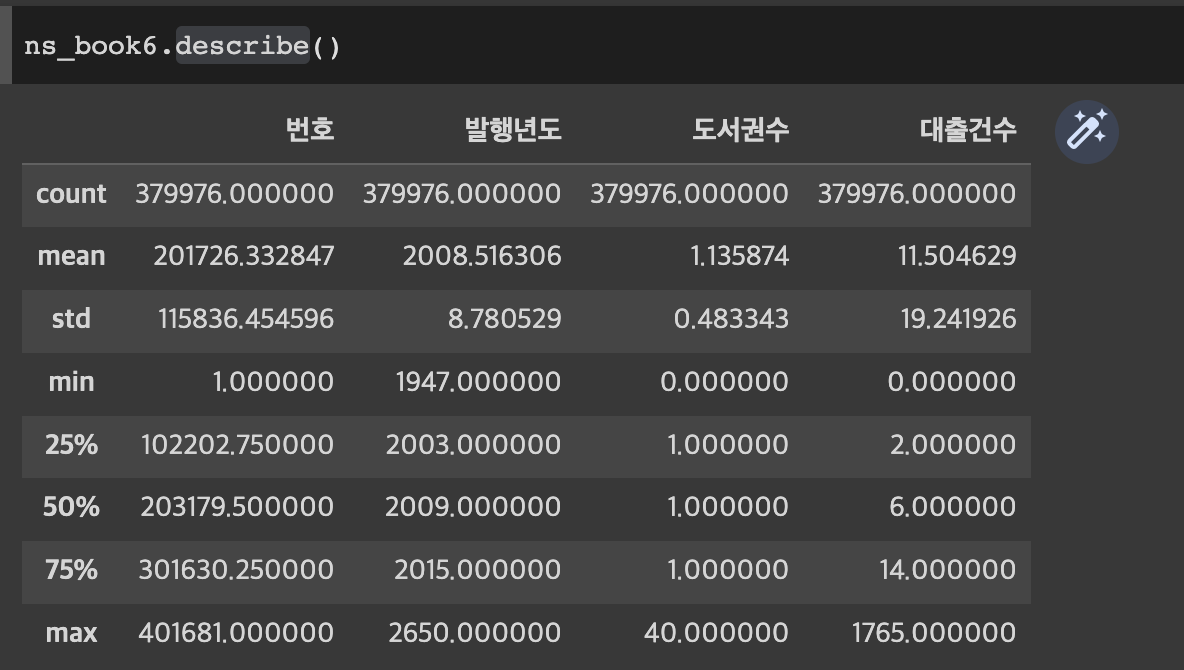
① 평균
- 정의 : 숫자값을 모두 더해 갯수로 나눈값
- 가장 기본적으로 알아보는 통계 지표
- mean() 메소드 이용
② 중앙값
- 정의 : 전체 데이터를 순서대로 늘어 놓았을때 중앙에 위치하는 값
(주의 : Value을 기준으로 중앙이 아닌 갯수 관점) - median() 메소드 이용
- 중복값을 제거하고 사용시에는 drop_duplicates().median() 의 방식을 이용
- 예시
- 1, 2, 5, 10, 20 일때의 중앙값은 5
- 1, 2, 3, 4 이렇게 짝수개 있을때는 2,3의 평균값인 2.5가 중앙값
③ 최솟값 ④ 최댓값
- 정의 : 가장 작은 값, 가장 큰 값을 의미함
- min(), max() 메소드를 이용함
⑤ 분위수
- 정의 : 데이터를 순서대로 늘어 놓았을때 이를 균등한 간격으로 나누는 기준점
- 이분위수, 사분위수 와 같은 용어가 이것을 의미하며, 이분위수는 2개로 나눈 기준점, 사분위수는 4개로 나눈 기준점을 의미합니다.
- quantile() 메소드를 사용함
⑥ 분산
- 정의 : 평균으로부터 데이터가 얼마나 퍼져 있는지를 나타내는 통계량
- 분산이 작다 : 데이터가 평균으로 부터 모여있음을 의미
- 분산이 크다 : 데이터가 평균으로 부터 퍼져있음을 의미
- 계산 방법 : 데이터의 각 값에서 평균을 뺀 다음 제곱한 후 평균처럼 갯수로 나누어지는 값
- var() 메소드를 사용
⑦ 표준편차
- 정의 : 위에서 설명한 분산값에 제곱근 즉 √ 를 적용한 값 입니다.
- 분산은 수치가 너무 크기 때문에, 제곱근으로 적당하게 줄여 사용하는데 이를 표준편차라 합니다. (즉, 표준편차2=분산)
- 분산보다는 일반적으로 표준편차를 더 많이 사용하는것 같습니다.
- std() 메소드를 사용
⑧ 최빈값
- 정의 : 데이터에서 가장 많이 등장(포함하고 있는) 값을 의미
- mode() 메소드 사용



